Go 高度平衡二元搜尋樹

tags: Go BinarySearchTree AVL Tree

category: 資料結構與演算法

description: Go 建立高度平衡二元搜尋樹

created_at: 2021/07/31 21:00:00

事前準備

• 知道什麼是二元搜尋樹
• 準備好想跟樹做好朋友的心
• 看過上一篇 Go 二元搜尋樹

前言

很久很久以前，還在高三擔任程式選手的時候，有使用過 VB 實作 AVL Tree，那次寫了一整個早上才做出來，成就感滿滿，這次想說用 Go 練練手，而過了好幾年，寫出來也簡潔很多。

目標

• 從上一篇 Go 二元搜尋樹 做延伸，實作 AVL Tree

高度平衡二元搜尋樹

先從二元搜尋樹最致命的缺點來看，如果你給他的資料順序剛好全部遞增或遞減，就會造成歪斜的狀況，就算不是全部剛好遞增或遞減，只要稍微有點歪斜，效率就會變得非常差。

如果你剛好使用 OOP 的方式建立一個完全歪斜的二元搜尋樹，那麼恭喜你，沒有浪費什麼空間，就只是找起來效率差的跟陣列一樣。

但是如果你剛好使用 Array 的方式去建立呢，那麼恭喜你，記憶體可能會爆炸。總之就是很浪費空間就是了。

基本上跟二元搜尋樹的規則一樣，只是加入了自平衡的特性。

先來看一下陣列通常怎麼存二元樹

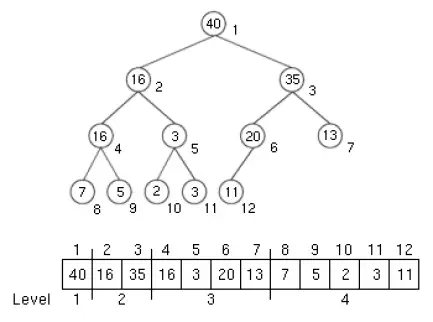
雖然說陣列從 0 開始編號，但是在存二元搜尋樹時，為了方便計算有時會刻意從 1 開始使用。 所以你可以發現各層的索引範圍

• 第一層: 1
• 第二層: 2 ~ 3
• 第三層: 4 ~ 7
• 第四層: 8 ~ 15
• 第N層 :

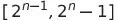
所以換句話說，如果你有4個節點的歪斜樹，你就需要開 2^4 大小的陣列。

• 如果你有10個節點，2^10=1024
• 如果你有65536個，2^65536=19729位數的數字

搜尋起來雖然跟陣列 O(N) 一樣的速度，但是你所花費的空間多上太多。 所以我們需要讓二元搜尋樹自己平衡，不要長歪。

在操作之前

操作之前我們必須知道，在他旋轉完成之後，中序走訪結果不能有任何改變，如果改變，代表旋轉的操作是錯誤的。

中序走訪結果不同，代表結構已經被破壞掉了

什麼情況下不平衡

當左子樹與右子樹的樹高差距大於 1 的時候

想當初學的時候書上會寫 平衡因子(BF, Balance Factor) 這種東西，就是 左子樹高 - 右子樹高 的結果。

如果根據上面定義，就可以知道說當 BF值 < 0 代表樹往右邊歪，反之則是往左邊歪，而正好等於零的情況則是完全沒有失衡。

AVL Tree 的四種操作

有點懶得找跟畫示意圖，總之照著上面說的，操作完之後中序走訪結果要相同。

LL 旋轉

當樹往左邊傾斜的時候，應該把左子樹拉上來

LR 旋轉

雖然樹往左邊傾斜，但是左子樹往右傾斜，就必須先救一下左子樹(右旋轉)再進行左旋轉，所以要做兩次旋轉。

偷懶一下，另外兩個當然就是的 RR 跟 RL 啦，跟上面相反，應該可以想像。

Go 實作

我們希望我們的 Node 具有 Balance() 方法 ， 負責把自己這個 子樹 平衡，而我們在每次新增節點都有可能造成失衡，所以要在新增最後吐回去 Balance 後的結果。

func (node *Node) Add(num int) *Node{
    if node == nil {
        return &Node{Value: num}
    }

    if num < node.Value {
        node.Left = node.Left.Add(num)
    } else {
        node.Right = node.Right.Add(num)
    }

    return node.Balance()
}

基本上只差在最後一行從回傳 node 變成 node.Balance()

在實作 Balance() 之前，我們需要先有辦法取得 BF值。

func (node *Node) GetBFValue() int {
    return node.Left.GetHeight() - node.Right.GetHeight()
}

在寫好了取得樹高的函數之後，要取得 BF值 相當容易。

核心程式碼

func (node *Node) Balance() *Node {
    value := node.GetBFValue()

    if math.Abs(float64(value)) <= 1 {
        return node
    }

    if value > 1 {
        checkValue := node.Left.GetBFValue()
        if checkValue < 0 {
            node.Left = node.Left.RightRotate()
        }
        return node.LeftRotate()
    } else {
        checkValue := node.Right.GetBFValue()
        if checkValue > 0 {
            node.Right = node.Right.LeftRotate()
        }
        return node.RightRotate()
    }
}

先取得 BF值 之後，再根據 BF值 去做相對應的處理，再來就是要實現左旋轉與右旋轉的函數，基本上就是對於指標的操作。

func (node *Node) LeftRotate() *Node {
    newRoot := &Node{Value: node.Left.Value}
    newRoot.Left = node.Left.Left
    newRoot.Right = node
    newRoot.Right.Left = node.Left.Right

    return newRoot
}

func (node *Node) RightRotate() *Node {
    newRoot := &Node{Value: node.Right.Value}
    newRoot.Right = node.Right.Right
    newRoot.Left = node
    newRoot.Left.Right = node.Right.Left

    return newRoot
}

到這裡就完成 AVL Tree 的實作了。

測試程式

nums := []int {1,2,3,4,5,6,7}
var tree BinarySearchTree
tree.BuildTree(nums)
fmt.Printf("Build tree: %v\n", nums)
fmt.Printf("tree.PreOrder = %v\n", tree.PreOrder())
fmt.Printf("tree.InOrder = %v\n", tree.InOrder())
fmt.Printf("tree.PostOrder = %v\n", tree.PostOrder())
fmt.Printf("tree.GetHeight = %v\n", tree.GetHeight())

tree.Add(8)
tree.Add(9)
tree.Add(10)
fmt.Printf("Insert node 8, 9, 10: \n")
fmt.Printf("tree.PreOrder = %v\n", tree.PreOrder())
fmt.Printf("tree.InOrder = %v\n", tree.InOrder())
fmt.Printf("tree.PostOrder = %v\n", tree.PostOrder())
fmt.Printf("tree.GetHeight = %v\n", tree.GetHeight())

輸出:

Build tree: [1 2 3 4 5 6 7]
tree.PreOrder = [4 2 1 3 6 5 7]
tree.InOrder = [1 2 3 4 5 6 7]
tree.PostOrder = [1 3 2 5 7 6 4]
tree.GetHeight = 3
Insert node 8, 9, 10:
tree.PreOrder = [4 2 1 3 8 6 5 7 9 10]
tree.InOrder = [1 2 3 4 5 6 7 8 9 10]
tree.PostOrder = [1 3 2 5 7 6 10 9 8 4]
tree.GetHeight = 4

會發現建立出來的結果相當完美，以往1234567，應該會造成一棵完全歪斜的高度為7的二元搜尋樹，被轉換成了長滿的二元搜尋樹。

而繼續一個一個新增節點，也照著我們的邏輯去做旋轉，沒有產生歪斜的情況。