Go 二元搜尋樹
tags: Go BinarySearchTree
category: 資料結構與演算法
description: Go 建立二元搜尋樹
created_at: 2021/07/31 05:00:00

事前準備
- 稍微學過一點資料結構或演算法
- 就算不會寫
Go至少要有其他程式語言基礎 或是你當英文看就好
前言
想當初大一上程式設計課的時候是上 Java,那時也是我第一次寫 Java,因為之前是程式選手的關係,也寫了不少樹與圖的題目,那時就使用 Java 寫了一個二元搜尋樹的類別,老師發現我做了這件事之後的表情與動作,至今我還是記得。
我自己是覺得從解題或實作一些資料結構與演算法學一個語言是滿適合的一件事,畢竟本來語言就只是一個工具,如果你已經知道你要做什麼,只是使用不同的語法寫出來而已。
目標
- 寫兩個類別,分別是
BinarySearchTree與Node - 可以增加節點
- 可以走訪 (前、中、後)序
- 可以取得樹高
這裡刻意拆成兩個類別,但如果要方便寫其實寫一個 Node 就可以,之前解題偷懶常常這麼做
樹
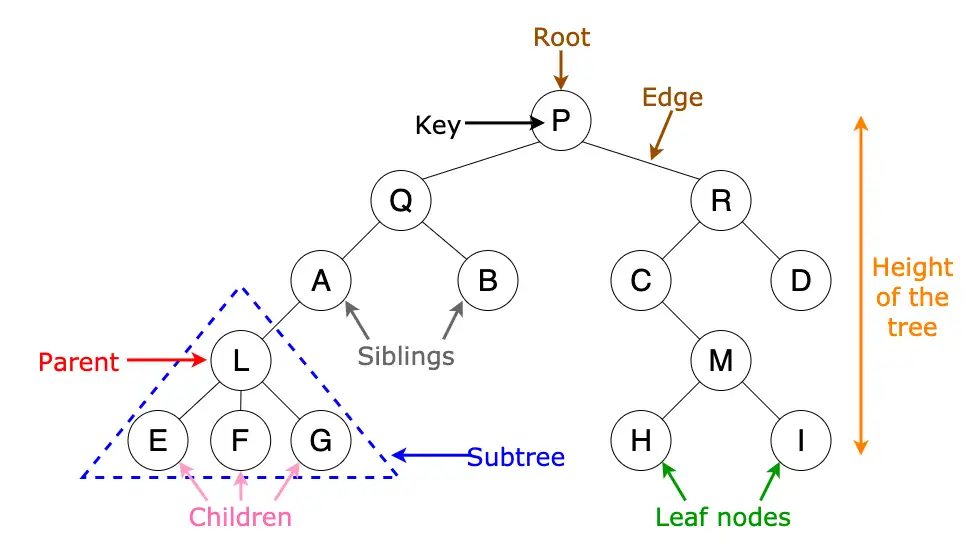
稍微解釋一下
- Root: 最上面的節點,只有一個,例如: P
- Key: 鍵,當資料或值看待,圈圈裡的東西
- Edge: 邊,通常圖可能表示成 G(V, E), 點與邊的集合,樹也是一種圖,如{P, R}代表 P 與 R 有一條線連起來
- Siblings: 兄弟節點,例如A、B
- Parent: 父親節點,簡稱父節點,對於E、F、G來說是L,對於A、B來說則是Q
- Children: 小孩,Parent會分這個應該就沒問題
- Subtree: 子樹,這就是為什麼用OOP(物件導向)做會很合適(可以稍微思考一下)
- Leaf: 樹葉(或稱 Terminal 終端)節點,最下面沒有小孩的節點,例如H、I
- Height: 高度,也有深度(depth)的定義,但是這點比較模糊,有些人0開始算有些人1開始算,
反正溝通的了就好
樹基本上是一種分治演算法的實現,而分治演算法基本上時間複雜度都不會太差。 大多平均時間複雜度都會跟logN扯上關係。
另外如果你對樹非常有興趣,跟高三時期的我一樣,也許可以嘗試做到log log N這樣瘋狂的樹,那棵樹很帥,叫做: van Emde Boas tree。
進入正題
什麼是二元搜尋樹
- 可以是空集合
- 如果不空,左邊的節點資料比較小
- 如果不空,右邊的節點比較大
例如
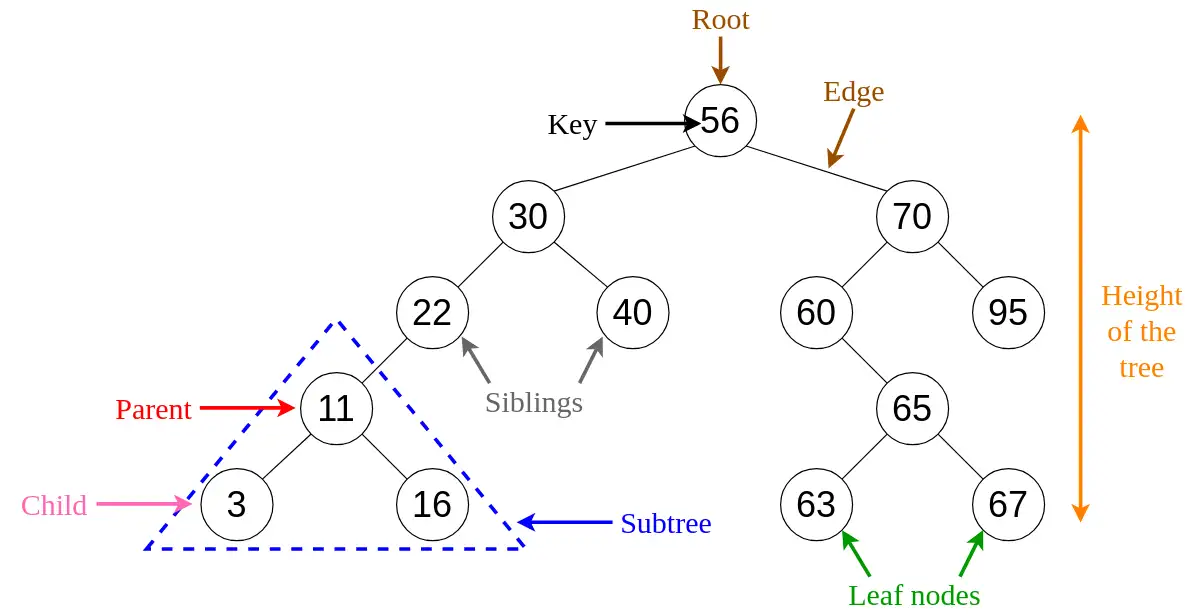
可以看到說
- 56 比 30 大 比 70 小
- 30 比 22 大 比 40 小
- 22 比 11 大
- 65 比 63 大 比 67 小
- ... 依此類推
所以他有一個規律在,可以想像一個下面這樣的結構 (當虛擬碼看就好)
struct Node {
left: Node
right: Node
value: int
}如果我的 left 也是一個 Node ,那麼我 left 的 left 也還是一個 Node,無限循環下去,那我只要保證一個 Node 做到二元搜尋樹的規則, 那麼整棵樹都會符合規則。
開始 Go 吧!
先定義結構(這邊故意把兩個類別拆開增加語意,但實際上一個類別就能更簡單做到)
type Node struct {
Left *Node
Right *Node
Value int
}
type BinarySearchTree struct {
*Node
}假設我預期這麼使用他
nums := []int {4, 2, 1, 6, 3, 7, 5}
var tree BinarySearchTree
tree.BuildTree(nums)- 先定義一個陣列當作資料
- 建立一個樹的變數
- 再來建立樹(把資料丟進去)
BuildTree
func (tree *BinarySearchTree) BuildTree(nums []int) {
if len(nums) == 0 {
log.Fatal("The length of nums cannot be 0.")
}
tree.Node = &Node{Value: nums[0]}
for _, num := range nums[1:] {
tree.Node = tree.Add(num)
}
}- 如果沒有丟資料進來,就輸出錯誤訊息
- 如果有資料,先把Root建立出來(第一個節點)
- 再跑一個迴圈把剩下的節點一個一個新增
Add
func (node *Node) Add(num int) *Node{
if node == nil {
return &Node{Value: num}
}
if num < node.Value {
node.Left = node.Left.Add(num)
} else {
node.Right = node.Right.Add(num)
}
return node
}- 2 ~ 4行: 遞迴結束條件
- 6 ~ 10行: 二元搜尋樹的核心
建立好之後,走訪就很簡單啦
func (tree *BinarySearchTree) PreOrder() []int {
var paths []int
tree.Node.PreOrder(&paths)
return paths
}
func (tree *BinarySearchTree) InOrder() []int {
var paths []int
tree.Node.InOrder(&paths)
return paths
}
func (tree *BinarySearchTree) PostOrder() []int {
var paths []int
tree.Node.PostOrder(&paths)
return paths
}
func (node *Node) PreOrder(paths *[]int) {
if node == nil {
return
}
*paths = append(*paths, node.Value)
node.Left.PreOrder(paths)
node.Right.PreOrder(paths)
}
func (node *Node) InOrder(paths *[]int) {
if node == nil {
return
}
node.Left.InOrder(paths)
*paths = append(*paths, node.Value)
node.Right.InOrder(paths)
}
func (node *Node) PostOrder(paths *[]int) {
if node == nil {
return
}
node.Left.PostOrder(paths)
node.Right.PostOrder(paths)
*paths = append(*paths, node.Value)
}這邊我選擇傳一個 paths 陣列進去紀錄走完的結果,最後在 main 在自己組成輸出字串。
最後取得樹高
func (tree *BinarySearchTree) GetHeight() int {
return tree.Node.GetHeight()
}
func (node *Node) GetHeight() int {
if node == nil {
return 0
}
return int(math.Max(float64(node.Left.GetHeight()), float64(node.Right.GetHeight()))) + 1
}樹高使用 遞迴 也是非常容易取得
最後來的 main 函數
func main() {
nums := []int {4, 2, 1, 6, 3, 7, 5}
var tree BinarySearchTree
tree.BuildTree(nums)
fmt.Printf("Build tree: %v\n", nums)
fmt.Printf("tree.PreOrder = %v\n", tree.PreOrder())
fmt.Printf("tree.InOrder = %v\n", tree.InOrder())
fmt.Printf("tree.PostOrder = %v\n", tree.PostOrder())
fmt.Printf("tree.GetHeight = %v\n", tree.GetHeight())
tree.Add(8)
fmt.Printf("Insert node 8: \n")
fmt.Printf("tree.PreOrder = %v\n", tree.PreOrder())
fmt.Printf("tree.InOrder = %v\n", tree.InOrder())
fmt.Printf("tree.PostOrder = %v\n", tree.PostOrder())
fmt.Printf("tree.GetHeight = %v\n", tree.GetHeight())
}輸出
Build tree: [4 2 1 6 3 7 5]
tree.PreOrder = [4 2 1 3 6 5 7]
tree.InOrder = [1 2 3 4 5 6 7]
tree.PostOrder = [1 3 2 5 7 6 4]
tree.GetHeight = 3
Insert node 8:
tree.PreOrder = [4 2 1 3 6 5 7 8]
tree.InOrder = [1 2 3 4 5 6 7 8]
tree.PostOrder = [1 3 2 5 8 7 6 4]
tree.GetHeight = 4總結
基本上都是用遞迴去實作,遞迴在某些情況下還滿好用的,也可以嘗試改寫成非遞迴版(迴圈版),在建立樹的時候難度不會高上太多,但在走訪上就會比較難,可能約莫10來行左右,但遞迴只要不到5行的程式碼。
之後有時間的時候改寫成 AVL 的版本,AVL Tree 是高度平衡二元搜尋樹,解決了二元搜尋樹在一些資料會長歪的問題。
長歪就會導致時間複雜度從很好的 O(logN) 變為 O(N),如果沒感覺的話就想像如果有65535筆資料,一般平均情況下可能找16次會找到,如果長歪則需要找65535次。