Shortest Distance After Road Addition Queries I

tags: JavaScript

category: LeetCode

description: LeetCode - Shortest Distance After Road Addition Queries I

created_at: 2024/11/27 21:00:00

題目連結: https://leetcode.com/problems/shortest-distance-after-road-addition-queries-i

前言

這一題是 2024/11/27 的 Daily 題目，而為什麼會忽然寫這一題呢? 不是因為它的難度，而是因為今天剛好想到了一個不錯的做法，所以很想寫下來記錄一下。

這個做法應該是受到了 Union Find 、 Bellman-Ford 與 Dijkstra 的啟發(?)，總之是有那麼一點點感覺

題目簡介

1. 有向無環圖
2. 每個節點預設都和下一個數字相連
3. 給你一個 N 代表有 N 個節點
4. 給你一個 queries 陣列，裡面是 [u, v] 代表要把 u 連到 v
5. 求出每個 queries 連接後的最短路徑(從頭走到尾，意思是 0 到 N-1)
6. 題目不會有回頭路，也就是說 u 一定比 v 小
   • 題外話: 一開始我不小心把題目想複雜了，老實說這次我沒有細看題目(因為今天整天有點不太舒服(可能沒睡好QQ))，所以我第一個想的 edge case 是有沒有一種可能是他交叉著連結果更短，後來敲進 test case 才發現他不會有這種情況；不過接下來的解法可以涵蓋這種情況。

我想到的解法是這樣的:

1. 用一個 disatnces 存在每個節點到 0 的最短距離
2. 用一個 effects 存放某個節點變化時，應該更新誰?
3. 於是當 u 連到 v 的時候，如果有更好，我們就把 v 的距離更新成 u 的距離+1，並且更新 effects，並往前更新 disatnces。 ((這樣講比較順，雖然寫起來不是這樣，總之我們後面會細說

雖然說題目不會有回頭路，但為了進一步驗證這個解法，所以特別用有回頭路的 test case 來說明。

文字描述可能有點抽象，我們來看看圖，假設今天 N = 10

你的初始狀態是這樣的:

0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9

這時你的 distances 是這樣的:

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

然後你的 effects 是這樣的:

[
    [1], // 0
    [2], // 1
    [3], // 2
    [4], // 3
    [5], // 4
    [6], // 5
    [7], // 6
    [8], // 7
    [9], // 8
    []   // 9
]

這代表當 1 有變化時，我們要更新 2，當 2 有變化時，我們要更新 3，以此類推。

接著假設有組資料長這樣:

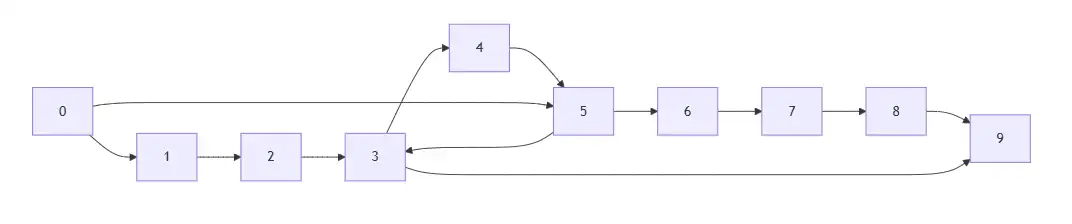
這邊是多了以下幾個資料:

[[3,9],[5,3],[0,5]]

以結果論來看，最短路徑是 0 -> 5 -> 3 -> 9，也就是 3。

那我們來看看這個 test case 的過程:

1. 當 3 連到 9 的時候，我們先更新 effects，當 3 有變化時，我們要更新 9，所以:

   [
    [1], // 0
    [2], // 1
    [3], // 2
    [4, 9], // 3
    [5], // 4
    [6], // 5
    [7], // 6
    [8], // 7
    [9], // 8
    []   // 9
   ]

接著需要去更新 distances，所以開始執行類似 Union Find 的操作:

索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
更新前: [0, 1, 2, 3, 4, 5, 6, 7 ,8, 9]
更新 4: [0, 1, 2, 3, 4, 5, 6, 7 ,8, 9] (略過，4沒有更優)
更新 9: [0, 1, 2, 3, 4, 5, 6, 7 ,8, 4] (更新)

接著我們再來看 5 連到 3 的時候:

[
    [1], // 0
    [2], // 1
    [3], // 2
    [4, 9], // 3
    [5], // 4
    [6, 3], // 5
    [7], // 6
    [8], // 7
    [9], // 8
    []   // 9
]

接著一樣更新 distances:

索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
更新前: [0, 1, 2, 3, 4, 5, 6, 7 ,8, 4]
更新 6: [0, 1, 2, 3, 4, 5, 6, 7 ,8, 4] (略過，6沒有更優)
更新 3: [0, 1, 2, 3, 4, 5, 6, 7 ,8, 4] (略過，3也沒有更優)

最後，我們再來看 0 連到 5 的時候:

[
    [1, 5], // 0
    [2], // 1
    [3], // 2
    [4, 9], // 3
    [5], // 4
    [6, 3], // 5
    [7], // 6
    [8], // 7
    [9], // 8
    []   // 9
]

接著一樣更新 distances:

索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
更新前: [0, 1, 2, 3, 4, 5, 6, 7 ,8, 4]
更新 1: [0, 1, 2, 3, 4, 5, 6, 7 ,8, 4] (略過，1沒有更優)
更新 5: [0, 1, 2, 3, 4, 1, 6, 7 ,8, 4] (更新)
    索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    更新 6: [0, 1, 2, 3, 4, 1, 2, 7 ,8, 4] (更新)
        索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
        更新 7: [0, 1, 2, 3, 4, 1, 2, 3 ,8, 4] (更新)
            索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
            更新 8: [0, 1, 2, 3, 4, 1, 2, 3 ,4, 4] (更新)
                索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
                更新 9: [0, 1, 2, 3, 4, 1, 2, 3 ,4, 4] (略過，9沒有更優)
    索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    更新 3: [0, 1, 2, 2, 4, 1, 2, 3 ,4, 4] (更新)
        索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
        更新 4: [0, 1, 2, 2, 3, 1, 2, 3 ,4, 4] (更新)
        索引  : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
        更新 9: [0, 1, 2, 2, 3, 1, 2, 3 ,4, 3] (更新)

這次的更新比較複雜，因為若有更優的話，我們就要一直往前更新，直到沒有更優為止，這樣才能保證整個 distances 是最優解。

如果有算法底子的這時可能就看出這樣的解法是 DFS，但其實這邊用 BFS 的話也可以做到一樣的結果，不過效率會有一些些差異，以這題的這個解法來說的話用 DFS 的話不只效率比較穩定，而且 Code 也比較好看(?)，但不管怎麼樣，這裡你用 DFS 還是 BFS 時間複雜度都是一樣的(以最壞情況來說，不過 DFS 可能不會)。

所以選擇 DFS 和 BFS 還是必須稍微評估一下，雖然大多數題目都是 BFS 比較快，但這題用 BFS 可能會導致前面都在做無謂的更新(queue越長越大)，如果用 DFS 就可以避免這種情況。

JavaScript 實作

一樣分段來解釋，首先定義 distances 與 effects，然後不要忘了最後要輸出的 output

const distances = Array.from({length: n}, (_, i) => i)
const effects = Array.from({length: n}, (_, i) => [i + 1])
const output = []

effects[n - 1] = []

接著我們需要開始讀取題目的 queries，這邊我們用 for 來讀取:

for (const [from, to] of queries) {
    effects[from].push(to)
    update(distances, effects, from)
    output.push(distances[n - 1])
}

最後我們需要實作 update，這邊我們用 DFS 來實作:

const update = (distances, effects, from) => {
    effects[from].forEach(node => {
        if (distances[node] > distances[from] + 1) {
            distances[node] = distances[from] + 1
            update(distances, effects, node)
        }
    })
}

這邊比較重要的是那個 if，這邊我們要判斷是否有更優解，如果有的話，我們就要一直往前更新，這樣不只能保證 distances 是最優解，也才不會拉垮整個時間複雜度。

最後我們就可以輸出 output 了:

return output

整個 Code 就這樣子，非常的精簡。

如果你要更精簡的話也許可以讓 update 直接使用 global 的 disatnces 和 effects

註: 使用遞迴的方式需要注意遞迴深度的問題，避免超過 Call Stack 的限制，不過這題資料不大，所以不用擔心這個問題；或者是你也可以單純使用 while + stack 來實作遞迴來避免這個問題。

最後附上 LeetCode 的截圖

然後他寫的時間複雜度是 O(N) 但其實這題最最最差的情況是 O(N^2)

(真的很差那種，要像下面這樣)

5
[[3,4],[2,3],[1,2],[0,1],[2,4],[1,3],[0,2],[1,4],[0,3],[0,4]]

漸漸的更新每一個，這樣 1 + 2 + 3 + 4 + ... + N，所以最差是 O(N^2)

不過這題的 N 最大是 500，所以這樣肯定超級快XD