LeetCode - 每天一題的挑戰(?)

tags: JavaScript

category: LeetCode

description: LeetCode - 每天一題的挑戰(?)

created_at: 2024/10/29 12:00:00

前言

一切都從去年的差不多這個時候開始(?)，當時覺得有點迷茫，想找點事情做，就開始了這個每天一題的挑戰，直到今天維持了一年，之後也是會繼續下去，所以沒意外明年的差不多這個時候也會有一篇類似的文章(?)

雖然過程中有幾天真的是要嘛忙要嘛忘(?)了漏掉，不過都有透過 LeetCode 上的 Time Travel Ticket 補回來就是了，但這樣的次數也沒有很頻繁，大概一隻手數的出來的次數而已(所以以一年來算失誤率大概是 1% 上下?)

這篇主要就是精選幾題很棒(?)的題目，然後其中過程也有碰到平台上很神奇的問題，也一併分享給大家。

先打個預防針，解法不見得是最好的，但至少是我自己覺得好讀好懂的(?)

先附上圖片(?)

中間那些灰灰的就是前面所說的使用 Time Travel Ticket 補回來的次數，希望明年可以全部都是亮的。

精選目錄(?)

• 數學(Math)
• 位元運算(Bit Manipulation)
• 陣列(Array)
• 鏈結串列(Linked List)
• 堆疊(Stack)
• 佇列(Queue)
• 兩個指標(Two Pointers)
• 滑動視窗(Sliding Window)
• 回溯法(Backtracking)
• 動態規劃(Dynamic Programming)
• 二分搜尋(Binary Search) 的另一種觀點(?)
• 深度優先搜尋(Depth First Search)
• 廣度優先搜尋(Breadth First Search)
• 字典樹 (Trie)
• 二元樹(Binary Tree)
• 神奇的 Daily
• 結語

好像有點多，但畢竟是一年的精華(?)

數學(Math)

題目: 592. Fraction Addition and Subtraction

這題是做數學分數的加減法，所以基本上就是把人類的分數加減法轉換成程式碼，例如:

• 通分
• 加減
• 約分 ...之類的

這題的輸入是一個字串，像是下面這樣:

1/3-1/2

所以第一個需要解決的問題是要如何把這個字串轉換成能夠處理的格式，比較直覺的就是將運算符的前後加上空白之後再用 split 來切割，類似像下面這種感覺:

const terms = X.replaceAll('+', ' + ').replaceAll('-',' - ').split(' ').filter(x => x)

這樣你會得到一個陣列，像是下面這樣:

[ '1/3', '-', '1/2' ]

這時你就可以一次拿出三個元素來做處理，像是下面這樣:

const [x, op, y] = terms.splice(0, 3)

不過這題可能會有前導的負號，所以一開始取代的時候可以將它排除在外，像是下面這樣來拿到正確的 terms:

const terms = (X[0] + X.slice(1).replaceAll('+', ' + ').replaceAll('-',' - ')).split(' ').filter(x => x)

這樣就算輸入的字串有前導負號也不會有問題了，假設輸入的字串是:

-1/2+1/2

這樣處理完之後就會得到:

[ '-1/2', '+', '1/2' ]

現在可以進入到人類的分數加減法了，我相信大家都會算，所以細節就不贅述了XD

首先我需要一個找最大公因數的函數，來幫助後面做通分和約分，這邊我們使用 輾轉相除法 來計算最大公因數:

1. 先找出兩個數中較大的數
2. 用較大的數去除以較小的數，如果餘數為 0，則較小的數就是最大公因數
3. 如果餘數不為 0，則將較小的數設為較大的數，將餘數設為較小的數，重複步驟 2

舉例來說，假設我們要計算 12 和 18 的最大公因數:

1. 先找出較大的數，也就是 18
2. 用 18 除以 12，餘數為 6
3. 將 12 設為 18，將 6 設為 12
4. 用 12 除以 6，餘數為 0
5. 因為餘數為 0，所以 6 就是 12 和 18 的最大公因數

但比較特別的是這邊需要做絕對值(abs)，因為數字可能有負數:

const gcd = (x, y) => {
    const min = Math.abs(Math.min(x, y))
    const max = Math.abs(Math.max(x, y))
    if (min === 0) return max
    return gcd(min, max % min)
}

接著一次拿出 terms 前面的三個值來做運算，算完之後塞回去，直到剩下一個值，這個值就是答案。

所以會像是下面這樣:

while (terms.length > 1) {
    const [x, op, y] = terms.splice(0, 3) // 一次拿出三個

    const [x1, x2] = x.split('/').map(x => +x) // 切完會是字串，所以要轉成數字
    const [y1, y2] = y.split('/').map(x => +x) // 切完會是字串，所以要轉成數字

    const ratio = gcd(x2, y2) // 找最大公因數
    const d = x2 * y2 / ratio // 通分的分母
    const n = x1 * y2 / ratio // 通分的分子(第一個數字)
    const m = x2 * y1 / ratio // 通分的分子(第二個數字)
    const r = op === '+' ? n + m : n - m // 加減

    const shrink = gcd(r, d) // 找最大公因數，用來約分
    terms.splice(0, 0, `${r / shrink}/${d / shrink}`) // 塞回去
}

這題與其說是 Math ，其實有點更像是模擬(Simulation)的題目，不過因為有些純 Math 的題目好像有點太水(?)或是有部分扯到dp(?)，所以就選了這題。

位元運算(Bit Manipulation)

題目: 2220. Minimum Bit Flips to Convert Number

上一題才說純 Math 的題目有點太水，這不就來了嗎，沒有啦，位元操作嘛難免。 當我沒說

這一題是這樣子的，給你兩個數字，問你要做幾次 XOR 操作才能把兩個數字變成一樣的，而一次只能對一個 bit 做 XOR 操作。

可以把他想成就是翻轉 bit，1 變成 0，0 變成 1，但是只能一次翻轉一個 bit，然後要做幾次的問題。

舉例來說:

10 = 1010
7 = 0111

可以透過下面的步驟，假設我要將 1010 變成 0111:

0. 1010
1. 0010
2. 0110
3. 0111

這樣透過三次的操作就可以將 1010 變成 0111 了。

反過來同理:

0. 0111
1. 1111
2. 1011
3. 1010

所以最最最直覺的辦法就是土法煉鋼，先將兩位數字轉為二進位並且對齊，然後一個一個 bit 去比較，去數看看有幾個不同的 bit，這樣就可以得到答案了。

var minBitFlips = function(start, goal) {
    const x = start.toString(2) // 轉成二進位
    const y = goal.toString(2) // 轉成二進位
    const maxLength = Math.max(x.length, y.length) // 取最大長度
    const padX = x.padStart(maxLength, '0') // 補零
    const padY = y.padStart(maxLength, '0') // 補零
    return Array(maxLength) // 建立一個長度為最大長度的陣列
        .fill(0) // 全部填 0，相當於初始化
        .filter((_, i) => padX[i] !== padY[i]) // 過濾不同的 bit，相當於計算有幾個不同的 bit
        .length  // 回傳長度(也就是有幾個不同的 bit)
};

但這樣的做法好像與我最前面所說的 Math 有點搭不上邊，所以我們來看看有沒有相對數學一點點的解法。或是專業一點點的寫法(?)

這邊我們可以透過 XOR 的特性來解這題，XOR 的特性是:

• 0 XOR 0 = 0
• 0 XOR 1 = 1
• 1 XOR 0 = 1
• 1 XOR 1 = 0

所以我們可以透過 XOR 來找出不同的 bit，然後再去數看看有幾個 1，這樣就可以得到答案了。

return (start ^ goal).toString(2) // XOR 並轉成二進位
                        .split('') // 轉成陣列
                        .filter(x => x == 1) // 過濾 1 的 bit
                        .length // 回傳長度

這樣剩下一行就可以解決這題了。好像也沒有數學到哪裡去(?)

陣列(Array)

題目: 1684. Count the Number of Consistent Strings

接著到了陣列的題目這題也是來水的，想把重點往後放...，這題是這樣子的，給你一個字串代表允許出現的字元，然後給你另一個陣列當中包含多個字串，看看有多少個字串只有出現前面所給的字元。

舉例來說:

allowed = "ab"
words = ["ad","bd","aaab","baa","badab"]

這邊只有 "aaab" 和 "baa" 是符合條件的，所以答案就是 2。

因為 ad 、 bd 和 badab 都有 d，然後 d 不在 allowed 中，所以這三個字串都不符合條件。

了解題意之後，這題就很簡單，將 allowed 轉成 Set，然後遍歷 words，對每個字串遍歷，看看每個字元是否都在 allowed 中，如果有一個不在就跳過，如果全部都在就加一。

建立好 Set 之後這題一樣可以透過一行解決:

return words
        .filter(word => 
            Array(word.length) // 建立一個長度為 word 長度的陣列
                .fill(0) // 全部填 0，相當於初始化
                .every((_, i) => set.has(word[i])) // 檢查每個字元是否都在 set 中
        ).length // 回傳長度

如果不習慣用 Array 的方法建立初始陣列再迭代，也可以直接將字串切成陣列，然後用 every 來檢查，至於切法隨你開心(?)，看你喜歡 word.split('') 還是 [...word] 都可以，或是乾脆用 for 迴圈也可以。

註: 建立 Array 之後迭代和直接切 word 之後迭代所消耗的空間是不同的，不過只要稍微知道就好，因為他們的差異微乎其微，幾乎可以不管，就看你開心，如果硬要的話，在這裡直接切 word 可能是比較好的選擇。

return words.filter(word => word.split('').every(c => set.has(c))).length

鏈結串列(Linked List)

題目: LeetCode 2807. Insert Greatest Common Divisors in Linked List

這題很單純，主要就是給了一個鏈結串列，然後要在每個節點中插入最大公因數，就像是下面這樣:

1. 一開始的鏈結串列:
2. 你要插入的最大公因數:
3. 插入後的鏈結串列:

相信這些圖已經足夠說明這題的意思了，接下來就是要實作了。

首先我們先實作一個函數來計算最大公因數:

const gcd = (x, y) => {
    const max = Math.max(x, y)
    const min = Math.min(x, y)
    if (min === 0) return max
    return gcd(min, max % min)
}

接著需要去走訪鏈結串列，並在每個節點中插入最大公因數:

let ptr = head
while (ptr.next) { // 如果還有下一個節點才需要插新的節點
    ptr.next = new ListNode(
        gcd(ptr.val, ptr.next.val),
        ptr.next
    ) // 把當前的下一個節點替換掉，替換的節點的下一個是原本的下一個
    ptr = ptr.next.next // 跳過新插入的節點往下走
}

上面這一段的行為有點像下面這樣: ptr只是代表當前在哪個節點，而不是 list-item

一開始的鏈結串列:

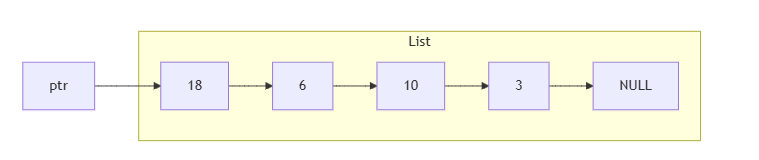
建立一個新的節點，值為 gcd(18, 6)，然後把新的節點的下一個節點設為原本的下一個節點:

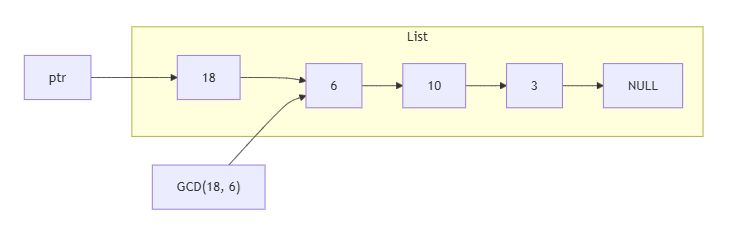
然後將當前的節點的下一個節點設為新插入的節點

然後將 ptr 設為新插入的節點的下一個節點，也就是原本的下一個節點

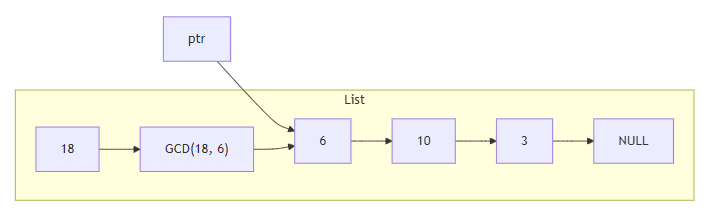
然後重複上面的步驟，直到沒有下一個節點為止

到這邊這題就解完了，這題滿適合拿來練習鏈結串列的操作，也是一個很好的題目(?)

堆疊(Stack)

題目: 1106. Parsing A Boolean Expression

說到堆疊問題，第一時間想到的可能是括號相關的問題，這題其實也算是一種括號問題的綜合版(?)

這題還滿可愛的，基本上也滿像是模擬人類的運算，去解析一個布林運算式最後的結果。

這題的布林運算式是這樣子的:

• t 代表 true
• f 代表 false
• !(expr) 代表 expr 的 not
• &(expr1, expr2, ..., exprn) 代表 expr1 到 exprn 的 and
• |(expr1, expr2, ..., exprn) 代表 expr1 到 exprn 的 or

然後題目會給你像是這樣的字串:

!(&(f,t))

這樣的字串代表的意思是:

not (false and true)

所以這樣的運算結果就是 true。

然後這時，一樣第一個問題是要如何將這個字串轉換成能夠處理的格式，這邊我們可以透過堆疊來解決這個問題。

我的想法是這樣的:

• 當碰到 ) 以外的東西都直接放進堆疊
• 當碰到 ) 時，就開始從堆疊中取出元素，直到遇到 ( 為止
• 算完之後再多取一個元素，這個元素就是運算子，運算完之後再放回堆疊

照上面這個步驟做的話會發現沒有 , 的用武之地，所以碰到 , 就跳過，不用理會。 幫,QQ

以上面的 !(&(f,t)) 來說，步驟如下:

1. ! 直接放進堆疊
2. ( 直接放進堆疊
3. & 直接放進堆疊
4. ( 直接放進堆疊
5. f 直接放進堆疊
6. , 跳過
7. t 直接放進堆疊
8. ) 開始運算

當到 ) 時，當前的堆疊長這樣:

[ '!', '(', '&', '(', 'f', 't' ]

這時就可以開始運算了，運算的方式就是一直從堆疊中取出元素，直到遇到 ( 為止，然後再多取一個元素，這個元素就是運算子，運算完之後再放回堆疊。

所以:

1. 取出 t 和 f，然後運算 t 和 f 的 and，得到 true
2. 將 true 放回堆疊 (記得轉成 t)

這時堆疊長這樣:

[ '!', '(', 't' ]

然後又讀到了一個 )，所以:

1. 取出 t，然後運算 t 的 not，得到 false
2. 將 false 放回堆疊 (記得轉成 f)

這時堆疊長這樣:

[ 'f' ]

這時堆疊中只剩下一個元素，這個元素就是答案了。 (記得轉回 true 或 false)

順完流程之後，接著就是實作，首先定義一個 stack 廢話:

const stack = []

接著開始走訪字串並處理:

for (const char of expression) {
    if (char === ',') continue // 跳過 `,`
    if (char !== ')') { // 如果不是 `)` 就直接放進堆疊並跳過運算
        stack.push(char)
        continue
    }

    // 這時肯定是 `)`，所以開始運算
    // 首先定義一個 `flag` 來記錄碰到的布林有哪些
    const flag = { t: false, f: false}

    // 取出堆疊中的元素，直到遇到 `(` 為止
    while (stack[stack.length - 1] !== '(') {
        const bool = stack.pop()
        flag[bool] = true // 把有出現的布林記錄下來
    }

    stack.pop()  // 多彈出一個 `(`
    const operation = stack.pop() // 取出運算子
    if (operation === '!') {
        stack.push(!flag.t ? 't' : 'f') // 運算 `not`，直接相反
    } else if (operation === '|') {
        stack.push(flag.t ? 't' : 'f') // 運算 `or`，只要有一個是 `true` 就是 `true`
    } else if (operation === '&') {
        stack.push(flag.f === false ? 't' : 'f') // 運算 `and`，沒有 `false` 就是 `true`
    }
}

然後最後一步就是回傳答案了:

return stack.pop() === 't'

這裡並沒有看到類似前面題目的 while，而且最後就這樣直接回傳，是因為題目保證了 expression 是合法的，所以掃完字串之後最後的堆疊中只會剩下一個元素，這個元素就是答案了，如果沒有保證合法，可能就要再多一些判斷，但我想這樣就不會是這題主要想考的考點了請去看括號匹配相關的題目等等...。

佇列(Queue)

嗯..我暫時想不到這一年有哪個題目是純粹的 queue 題目，所以請看 BFS 的部分吧，因為 BFS 通常都是使用 queue 去實作的。

兩個指標(Two Pointers)

題目: 881. Boats to Save People

這題是滿經典的題目(?)，給你一堆人的重量還有船能夠承擔的重量，然後一艘船最多只能載兩個人，問你最少需要多少艘船才能把所有人都載走。

這題的解法是透過兩個指標來解決，一個指向最重的人，一個指向最輕的人，先嘗試載重的人，再嘗試載輕的人，如果可以一起載就一起載，如果不能就只能載重的人，然後繼續往下走。

而這題的重量一開始並沒有排序，所以我們需要先排序，才能確定哪邊是輕哪邊是重。

const sortedPeople = people.sort((x, y) => x - y)

接著使用兩個指標(l、r)，分別從頭和尾開始向內縮:

let l = 0
let r = sortedPeople.length - 1
let output = 0
while (l <= r) {
    let value = 0
    if (sortedPeople[r] + value <= limit) { // 看看能不能載重的人
        value += sortedPeople[r--]
    }

    if (sortedPeople[l] + value <= limit) { // 看看能不能載輕的人
        value += sortedPeople[l++]
    }

    output++
}

return output

這時會發現第一個 if 是多餘的，但是可以在讀的時候更符合一開始的邏輯(先嘗試載重的人)，也可以將他刪除，因為總是至少可以載走重的(題目保證)。

while (l <= r) {
    let value = sortedPeople[r--] // 總是先載重的

    if (sortedPeople[l] + value <= limit) { // 看看能不能一起載走輕的人
        value += sortedPeople[l++]
    }

    output++
}

這時語意就有點跑掉了(value)，這時可以稍微重構一下:

while (l <= r) {
    if (sortedPeople[l] + sortedPeople[r] <= limit) { // 看看能不能一起載走
        l++ // 可以的話輕的被載走，所以代表輕的指標往內縮
    }

    output++
    r-- // 重的總是被載走
}

然後最後一行 r-- 總是會發生，所以可以放到其他地方(?)，像是下面這樣:

while (l <= r) {
    if (sortedPeople[l] + sortedPeople[r--] <= limit) {
        l++
    }

    output++
}

這樣又少了一行，這題大概就這樣了，也可以練習看看一些變化，例如不只可以載兩個人之類的。

滑動視窗(Sliding Window)

題目: 3. Longest Substring Without Repeating Characters

滑動視窗其實是兩個指標的一種應用，這題是一個經典的題目，給你一個字串，問你最長的不重複子字串的長度(只能有不同的字元組成的字串)。

例如 abcabcbb 的最長不重複子字串是 abc，所以答案就是 3，或是 pwwkew 的最長不重複子字串是 wke，所以答案也是 3。

這題就可以使用滑動視窗的技巧，透過兩個指標來解決，一個走在後面(l)，一個走在前面(r)，然後當發現 r 的字元已經重複了，就將 l 往前移動，直到 r 的字元不重複為止，然後在這個過程中不斷更新最長的長度。

一開始可以先將邊際條件處理好:

if (s.length <= 1) return s.length

當字串長度小於等於 1 時，直接回傳長度即可，因為不可能有重複的字元。

接著為了要快速的判斷字元是否重複，可以使用 Set 來處理:

const set = new Set()

然後定義需要的變數:

let l = 0
let r = 0
let len = 0

接著寫個迴圈:

while (r < s.length) { // 當 r 還沒走到底
    while (set.has(s[r])) { // 當 r 的字元已經重複
        set.delete(s[l++]) // 將 l 的字元從 set 中刪除，並將 l 往前移動
    }
    set.add(s[r++]) // 將 r 的字元加入 set，並將 r 往前移動
    len = Math.max(len, r - l) // 更新最長長度
}

最後那個 len 就是答案了。

回溯法(Backtracking)

回溯法的經典題目不外乎就是 N 皇后問題，但這邊當然不可能這麼水

不過回溯法其實就是一個 DFS 的應用，所以...你懂得，直接去看 DFS 吧。

這樣是不是有點太水了(?)，沒有啦，繼續往下看。

題目: 79. Word Search

其實說來說去，單純的回溯法就是一種暴力法，就是一直嘗試，直到找到答案為止，這題就是一個很好的例子。

這題是給你一個迷宮，迷宮裡面每一格都是一個字元，問你能不能走出特定的字串，而且只能往上下左右走，不能走斜的。

這題就可以透過回溯法來解決，一直嘗試走，直到找到答案為止。

所以這題想法就很簡單，先找到起點，然後開始 dfs，所以一開始會先需要找到起點:

for (let i = 0; i < board.length; i++) {
    for (let j = 0; j < board[i].length; j++) {
        if (board[i][j] === word[0]) { // 找到起點
            board[i][j] = '' // 暫時將走過的地方標記起來
            if (dfs(1, j, i)) return true //如果找到答案就直接回傳
            board[i][j] = word[0] // 恢復原本的字元
        }
    }
}

return false  // 如果都沒有找到就回傳 false

接著需要一個 dfs 函數:

const dx = [1, -1, 0, 0] // x方向
const dy = [0, 0, 1, -1] // y方向
const dfs = (wi, x, y) => { // 分別為目前字串的位置、x座標、y座標
    if (wi === word.length) return true // 如果 wi 已經等於 word 長度，代表找到答案了
    for (let i = 0; i < 4; i++) {  // 分別走四個方向
        const newX = x + dx[i] // 新的 x 座標
        const newY = y + dy[i] // 新的 y 座標
        if (typeof board[newY]?.[newX] === 'undefined') continue // 如果超出邊界就跳過
        if (board[newY][newX] === word[wi]) { // 如果找到下一個字元
            board[newY][newX] = '' // 暫時將走過的地方標記起來
            if (dfs(wi + 1, newX, newY)) return true // 如果找到答案就直接回傳
            board[newY][newX] = word[wi] // 恢復原本的字元
        }
    }

    return false // 如果都沒有找到就回傳 false
}

在這段程式中，typeof 那一行算是比較暴力的判斷方法，透過 Optional chaining 的方式來判斷是否超出邊界，因為超出就會拿到 undefined，所以這樣就可以避免 index out of range 的問題。

如果不習慣或不想用的話也可以使用比較早期的判斷 length 的方式來處理，這樣也是可以的。

至於為什麼說比較暴力呢?，因為 Optional chaining 可能會有一點點的效能問題，雖然適度使用可以提高開發體驗與提高程式碼的可讀性，但過度使用可能會有反效果。

雖然說是效能問題，但適度使用也不用太過擔心，大概就從 LeetCode 的 Accepted 變成 Time Limit Exceeded 而已(?)。

所以有時如果在 LeetCode 上遇到 Time Limit Exceeded 的問題，然後又用了這個 Optional chaining 的技巧，也許可以嘗試看看用比較原始的方式來處理，說不定有機會被你矇到就過了(x)，雖然可能通常都是演算法要修正就是了，就好比 ICPC 通常不是語言的問題一樣。

註: 我並不是說 typeof 效能不好，而是 Optional chaining；但要在效能和可讀性之間做取捨

動態規劃(Dynamic Programming)

終於到了動態規劃，這個實在不是很好處理，有些時候就是一個「感覺」，如果一開始方向不對，真的永遠都解不出來，但是相反的，只要看出他的規律，方向對了，就能夠順利解出來。

因為有時簡單的 dp 可能會落入 greedy 的陷阱，而有時複雜的 dp 可能又會因為沒想清楚而導致過高的時間複雜度(也許是重疊子問題沒有處理好)。

題目: 931. Minimum Falling Path Sum

挑了一個比較直覺但又不太水的 dp 題目(?)，這題是給你一個二維陣列，然後問你從最上面那列走到最下面那列的最小路徑和，每次只能往下走一格或是往左下或是往右下走一格。

所以很直覺的，每次的答案都會從上一列的最小值加上當前的值，而那個最小的值只在上一列的三個值中選擇。

然後最後一列的最小值就是答案了。

可以想像每一層的每一個值都是從最上面走到當前位置的最小路徑和。

我知道說到這邊有點抽象，但這就是 dp 的感覺，所以直接來看程式碼吧。

首先定義初始狀態，也就是第一列，如同剛才前面說的，每一列的每一個值都是從最上面走到當前位置的最小路徑和，所以第一列就是第一列的值:

const dp = Array(matrix.length).fill(0).map(() => Array(matrix[0].length).fill(0))
for (let i = 0; i < matrix[0].length; i++) {
    dp[0][i] = matrix[0][i]
}

之後從第 i=1，也就是第二層開始往下走，而每一層都會依據前一層的值來找出最優的解:

for (let i = 1; i < matrix.length; i++) { // 從第一層走
    for (let j = 0; j < matrix[i].length; j++) { // 從左到右走
        const candidates = [
            dp[i-1][j]
        ] // 一開始候選值只有上一層同一欄的值，因為保證不會 index out of range
        if (j > 0) { // 如果當前這欄不是最左邊
            candidates.push(dp[i-1][j-1]) // 左上角的值加進候選中
        }

        if (j + 1 < dp[i].length) { // 如果當前這欄不是最右邊
            candidates.push(dp[i-1][j+1]) // 右上角的值加進候選中
        }

        dp[i][j] = Math.min(...candidates) + matrix[i][j] // 選擇最小的值加上當前的值
    }
}

最後最後，最後一列的最小值就是答案了:

return Math.min(...dp[dp.length-1])

二分搜尋(Binary Search) 的另一種觀點(?)

二分搜尋是一個很經典的搜尋方法，但如果只是單純的二分搜尋或是單純的找最左側的值做插入(python 還有 bisect 模組)，那就太無聊了。

不過老實說，在做到這一題之前，我還真沒用過這個觀點去看二分搜尋，所以也在這邊分享一下，但說不定你早就知道了也說不定，。

究竟是什麼觀點那麼神奇?，也許是我才疏學淺，自以為很神奇，但其實大家都知道QQ

就是一般來說二分搜尋都是以搜尋「值」為主體，而不是以「答案」為主體。 (<-- 至少我是這樣想的，也許用詞不是那麼精確

又或者是說，一般二分搜尋都用在解決問題的過程來加速而不是解決問題的答案

如果要比喻的話，我感覺有點像

• 從原始碼的視角，跳到架構的視角 (從單個檔案到整個專案)
• 從 CQS，昇華到 CQRS (Command Query Responsibility Segregation) (從函數到模組)

這樣的感覺，但這樣的比喻可能有點牽強。

總之扯遠了，我想表達的只是更往上一層的觀點，而不只是那麼的細節。

講了這麼多，上題目。

題目: 1482. Minimum Number of Days to Make m Bouquets

這題是給你一個陣列，這個陣列代表各個花開花需要的天數，然後給你一個 m 代表你需要的花束的數量，然後 k 代表一束花需要的花朵數量(需連續)，然後問你最少需要多少天才能夠做出 m 個花束。

舉例來說:

bloomDay = [1,10,3,10,2], m = 3, k = 1

這代表說我想要做出 3 個花束，每束需要 1 朵花，然後花開花需要的天數分別是 1,10,3,10,2，問我最少需要多少天才能夠做出 3 個花束。

所以在第一天的時候，只有第一朵花開了，然後第二天的時候，最後一朵花開了，然後第三天的時候，中間那朵花開了，像是下面這樣(紅色代表開花了):

• day 1: [1, 10, 3, 10, 2]
• day 2: [1, 10, 3, 10, 2]
• day 3: [1, 10, 3, 10, 2]

所以需要 3 天才能夠做出 3 個花束，所以答案就是 3。

這個例子一個花束只需要一朵花，可能沒有連續的感覺，所以換下一組例子:

bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3

這個例子代表說我想要做出 2 個花束，每束需要連續的 3 朵花，然後花開花需要的天數分別是 7,7,7,7,12,7,7，問我最少需要多少天才能夠做出 2 個花束。

所以會像下面這樣

• day 6: [7, 7, 7, 7, 12, 7, 7] (哪一朵都沒開)
• day 7: [7, 7, 7, 7, 12, 7, 7] (一瞬間開了6朵)
• day 12: [7, 7, 7, 7, 12, 7, 7] (花全開了)

這邊可以看到他在第 7 天的時候一瞬間開了 6 朵花，但是因為並沒有連續 2 個 3 朵花，所以這不是答案。

直到等到第 12 天的時候，才能夠做出 2 個花束，因為找的到 2 個連續的 3 朵花，所以答案就是 12。

我們先來看看題目的限制:

bloomDay.length == n
1 <= n <= 10^5
1 <= bloomDay[i] <= 10^9
1 <= m <= 10^6
1 <= k <= n

這題的解法就是透過二分搜尋來解決，而這邊的二分搜尋是以「答案」為主體，而不是以「值」為主體。

而答案就是那一個天數，也就是 10^9 以內的一個數字，看似好像很大會超時，但透過二分搜尋，也就是 log(10^9) ~= 30 次就可以找到答案。

而一次再去透過一個 O(n) 的迭代去檢查是否可以做出 m 個花束，所以整體的時間複雜度就是 O(nlogn)。 (<--變數沒有用的很精確，但大概就是這樣)

註: 基本上在 LeetCode 上面的題目，O(nlogn) 的時間複雜度是可以接受的。但 O(n^2) 就不好說了

接著來看 Code 吧。

首先，先排除邊際條件，絕對做不出來的情況:

if (m * k > bloomDay.length) return -1

如果一束花的花朵數量乘上花束數量大於花的總數量，那就絕對做不出來，所以直接回傳 -1。

接著二分搜尋的上下界分別就是 1 和 10^9，然後開始二分搜尋:

let l = 1
let r = 10 ** 9
while (l <= r) {
    const mid = l + Math.floor((r - l) / 2) // 取中間值
    // 產生一個花束的陣列，如果已經開花就是 `x`，否則是 `_`
    const flowers = bloomDay.map(d => d <= mid ? 'x' : '_') 
    // 算出可以做出的花束數量
    const value = M(flowers, k)

    if (value < m) { // 花束不夠，嘗試往右邊找
        l = mid + 1
    } else { // 花束太多或剛好，嘗試往左邊找出最少天數
        r = mid - 1
    }
}

// 跳出迴圈時，`l` 就是答案
return l

這時那個 M 函數就是用來計算可以做出的花束數量，我知道取名可能不是很好，但解題就是這樣嘛(x)。

const M = (flowers, k) => {
    let count = 0
    let l = 0
    let r = 0
    while (r <= flowers.length) {
        // 如果找到連續 `k` 個 `x`，代表可以做出一束花
        if (r - l === k) {
            count++ // 花束數量加一
            l += k // 左指標往前移動 `k` 格
            r = l // 右指標移到左指標的位置，代表一個新的花束檢查
            continue
        }

        if (flowers[r] === 'x') { // 如果開花了
            r++
        } else { // 如果沒開花
            l = r + 1 // 左指標移到右指標的下一格
            r = l // 右指標移到左指標的位置，代表一個新的花束檢查
        }
    }
    return count // 回傳花束數量
}

這樣的話就可以在 O(n) 的時間複雜度去計算出可以做出的花束數量，然後透過二分搜尋去找出最少天數，最後得出來的時間複雜度就是 O(nlogn)。

一開始初始化的 r 也可以設定成 bloomDay 中最大的值，這樣就不用寫死 10^9，這樣也可以避免一些不必要的計算(當最大值約<(10^9)/2時)。

舉例來說，就算今天給的陣列很長，但是 bloomDay 的最大值超級小，那你的二分搜尋可能跑沒幾次就有結果了，但如果寫死 10^9，那就會跑約莫 30 次，才會有結果。

深度優先搜尋(Depth First Search)

來到了這個跟 backtracking 很像的 DFS，DFS 是一個很常用的搜尋方法，總之就是先走再說，撞牆了再退回來，然後繼續走，像是數字的全排列就是一個很經典的題目。

題目: 386. Lexicographical Numbers

這題是要你產生一個以字串排序的數值(從1到n)，舉例來說:

n = 13

這時的答案就是:

[1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9]

其實他就是建立一棵樹，長得像下面這樣:

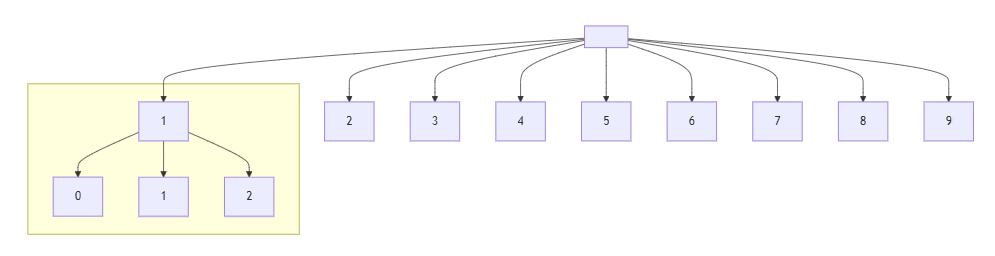
這棵樹是無根樹，其實他也是一個 Trie，只是他的每一個值我都要。

從根節點(最上面)開始，然後一路往左下走，也就是先從 1 開始，走到底之後再往上走，所以順序就會跟答案一模一樣。

這題就是一個很經典的 DFS 題目，如下:

var lexicalOrder = function(n) {
    const output = [] // 結果
    const dfs = (m) => { // 假設 m 是當前的數值
        if (m > n) return // 如果 m 大於 n 就結束
        output.push(m) // 將 m 加入結果
        const next = m * 10 // 下一個數值
        dfs(next) // 往左下走
        for (let i = 1; i <= 9; i++) {
            dfs(next + i) // 往右走
        }
    }
    // 無根樹，第一層是 1 ~ 9
    for (let i = 1; i <= 9; i++) { 
        dfs(i) // 從每一個數值開始
    }
    return output
};

這... DFS 我也不知道該怎麼用文字描述，畢竟使用到遞迴，而遞迴這種東西，當你開竅了就會理解，開竅前請多多練習，如果我只這樣說好像有點不負責任(x)，所以還是意思一下附上之前的文章，雖然不是主要講遞迴，但是有提到一點點遞迴的過程，或許可以參考一下，在當中的 2630. Memoize II 部分。

不過為什麼我會這麼說呢? 因為從前帶選手的時候常常需要從 0 到 1，但是對於真的完全是 0 的選手我真的也無能為力(畢竟如果連程式都害怕，不敢寫，真的是沒轍..)，我需要選手至少達到可以把自己的想法翻譯成程式碼，這樣我才有辦法讓他理解，進而翻譯成程式碼，讓選手迅速進步(?)，但是那個前期的過程真的只能靠自己，所以我才會這樣說。

如果能有讓人直接從這個 0 到 0.1 的萬靈丹，請跟我說，我很想知道

或者是這邊直接稍微做個簡要說明一下遞迴，總之就是一直呼叫自己，然後在適當的時機結束，這樣就可以達到目的。

以這個例子來說，結束的時機就是當數字大於 n 的時候，這時就可以結束了。

否則的話就先把自己加到結果陣列中，然後往下走(*10)，然後再往右走(+1)，這樣就可以達到目的了。

然後這題有一個額外說明: You must write an algorithm that runs in O(n) time and uses O(1) extra space.，但其實 LeetCode 上的題目這樣說，其實他也沒真的去驗，所以你可以不用管他，或是其實這點在討論區也滿有爭議(?)，常見的爭議如下:

• 答案就是一個陣列，所以額外O(1)不可能。當然可以把答案排除在外來說額外O(1)，就沒有違反
• 你使用遞迴，遞迴本身 stack 就不是O(1)的空間複雜度。也許可以說他的O(1)只針對變數並不針對呼叫堆疊

不管怎麼樣，總之要練習的點到位就好，這些小細節可能並不是那麼重要。

當然，你也可以無視這項規定，然後透過下面這一行解掉這個問題:LeetCode: 沒禮貌

return Array(n).fill(0).map((_, i) => i + 1).sort()

因為這題的限制很佛心，只有 1 <= n <= 5 * 10^4，所以你直接字串排序也是可以的，但是這樣就失去了這題的意義了。

如果這題狠一點，把測資放大，那就沒辦法這樣了。

廣度優先搜尋(Breadth First Search)

說完了 DFS，當然也要說說 BFS，BFS 就是一層一層的走，先走完一層再走下一層，你也可以理解成倒水的擴散方式，先擴散一層再擴散下一層。

那麼既然是這種擴散方式，就很適合使用 queue 來處理，因為 queue 就是先進先出，先看到的值就是先處理的。

題目: 2641. Cousins in Binary Tree II

這題是要你把二元樹當中的值做更新，更新的方式是把你的值變成表兄弟節點的和，表兄弟節點就是同一層的節點但是不同父節點。

假設以下面這棵樹來說:

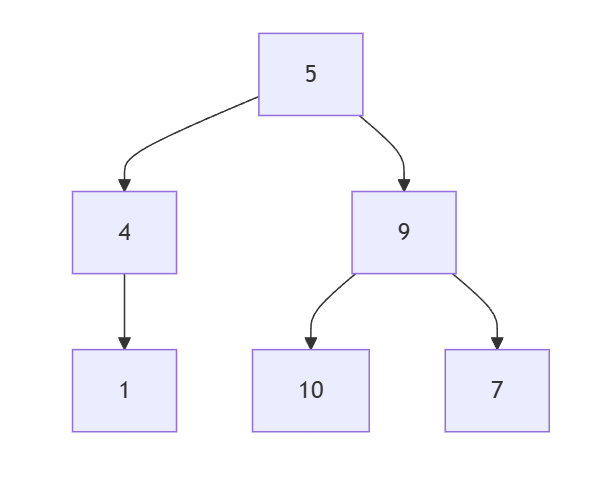
要不同父節點，所以你可以明確看出來最上面兩層的節點，也就是5、4、9，他們沒有表兄弟節點，所以他們的值會歸零。

然後對於下一層的 1 來說，他的表兄弟節點就是右邊的 10 和 7，所以他的值就是 10 + 7 = 17。

反之亦然，對於 10 和 7 來說，他們的表兄弟節點就是 1，所以他們的值就是 1。

所以運算後會變成這樣:

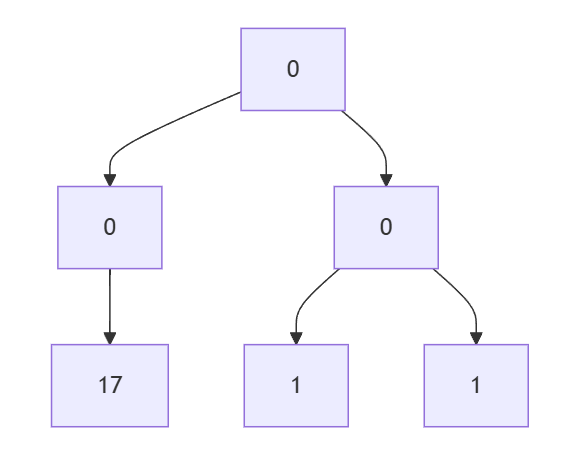
接著來看更高的樹:

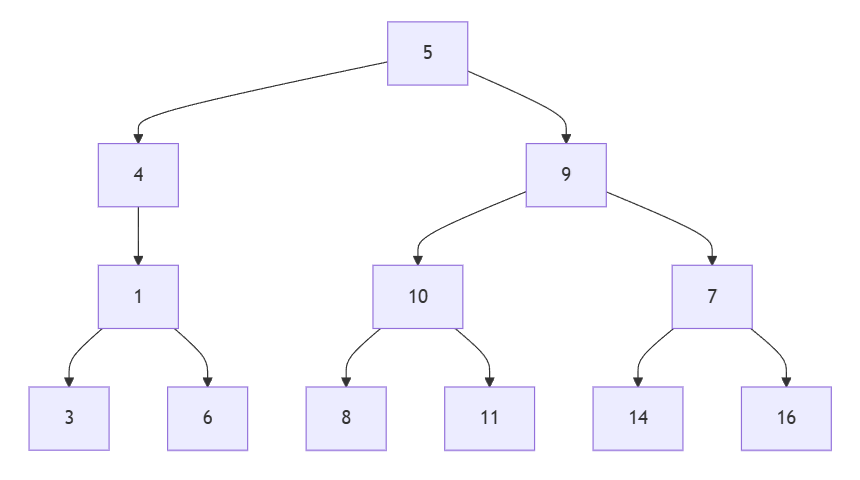
這時可以看到以最下面那一層來說，最左側的 3 和 6 應該會是右邊的值 8 + 11 + 14 + 16 的總和。 中間的 8 和 11 也是一樣，他們的值應該是 3 + 6 + 14 + 16 的總和。 最後是右邊的 14 和 16，他們的值應該是 3 + 6 + 8 + 11 的總和。

所以以直覺來說，可以先把每一層的值加起來，然後扣掉自己所屬的節點(包含你的兄弟)的值，就是你要更新的值了。

兄弟節點的意思是同一層且同一個父節點的值，所以以上例來說，可以先求出同一層所有的值的總和: 3 + 6 + 8 + 11 + 14 + 16 = 58

然後由左而右分別是:

• 58 - 3 - 6 = 49
• 58 - 8 - 11 = 39
• 58 - 14 - 16 = 28

這樣就可以得到答案了。

接著來看程式碼，首先我要取得各層的總和

const getLevelSum = (root) => {
    const levelSum = []
    const queue = [[root, 0]] // 分別代表節點和深度
    while (queue.length) { // BFS，如果 queue 還有資料就繼續
        const [node, depth] = queue.shift() // 取出第一個見到的節點和深度
        levelSum[depth] = (levelSum[depth] || 0) + node.val // 將節點的值加到對應的深度
        if (node.left) queue.push([node.left, depth + 1]) // 如果有左節點就加到 queue 中，並且深度+1
        if (node.right) queue.push([node.right, depth + 1]) // 如果有右節點就加到 queue 中，並且深度+1
    }
    return levelSum // 回傳各層的總和
}

const levelSum = getLevelSum(root) // 取得各層的總和

接著我希望從根節點開始，每一層的父節點負責更新子節點的值，這樣比較好管理兄弟節點，來做到前面所提到的更新方式。

所以這樣的話邊際就是我的根節點不會被更新，所以首先要將他設為 0，然後再來更新每一層的值:

root.val = 0  // 根節點不會被更新，先設為 0
const queue = [[root, 1]] // 從根節點開始，更新的層數從 1 開始
while (queue.length) { // BFS，如果 queue 還有資料就繼續
    const [node, depth] = queue.shift() // 取出第一個見到的節點和深度
    let sum = 0 // 兄弟節點的總和
    if (node.left) sum += node.left.val  // 如果有左節點就加到總和中
    if (node.right) sum += node.right.val // 如果有右節點就加到總和中
    if (node.left) { // 如果有左節點
        node.left.val = levelSum[depth] - sum // 更新左節點的值
        queue.push([node.left, depth + 1]) // 將左節點加到 queue 中，並且深度+1
    }
    if (node.right) { // 如果有右節點
        node.right.val = levelSum[depth] - sum // 更新右節點的值
        queue.push([node.right, depth + 1]) // 將右節點加到 queue 中，並且深度+1
    }
}

return root // 回傳更新後的樹

相信這樣的寫法是很直覺的，雖然也有 one-pass 的寫法，但是這樣的寫法比較直覺，也比較好理解。

而且時間複雜度相同，雖然硬要說的話 one-pass 的寫法可能會跑比較快，但效能和可讀性之間的取捨，這就要看你自己的需求了。

字典樹 (Trie)

接著是相對於二元樹可能比較少見的 Trie，Trie 是一種樹狀結構，用來儲存字典或是前綴樹，這樣的結構可以讓你快速的查詢字串是否存在於字典中，或是查詢是否有符合前綴的字串。

雖然說是這樣說，但常常可能都有其他方式可以不用自己實作 Trie 的資料結構來解題

題目: 1233. Remove Sub-Folders from the Filesystem

這題是要你模擬移除資料夾，我們知道檔案系統中是樹狀結構，當你建立了資料夾，裡面包含資料夾或檔案，你刪除了最外面的資料夾，裡面的東西也會被刪除。

以這個例子來說:

folder = ["/a","/a/b","/c/d","/c/d/e","/c/f"]

他其實長得像這樣:

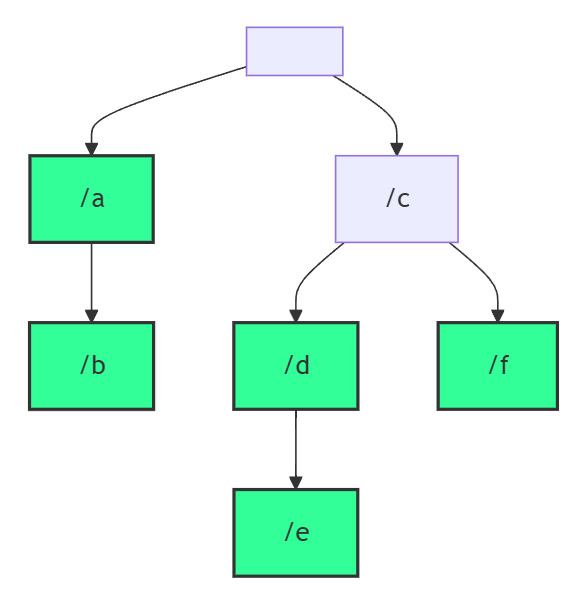
其中綠色的節點代表有值的節點，也就是你可以刪除的資料夾，而其他都只是路徑而已。

所以以這個例子來說，你可以刪除 /a 、 /c/d 和 /c/f 來讓全部的路徑都被刪除。

雖然有點違反直覺，因為如果以真實在使用的情境應該刪除 /a 和 /c 就可以了，不過這題的話只能刪除他有給的路徑。

也就是像下面這張圖: 紅色是你最少要刪除的部分:

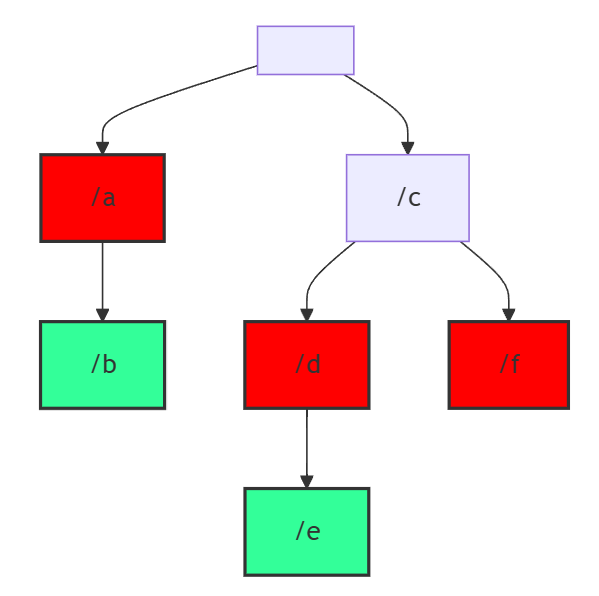
想必應該也注意到了，Trie是一個沒有根節點的樹狀結構，然後你建立好之後，基本上只要以 DFS 的方式走，走到有值的節點就退回來，後面就不必再走，所以這一題其實算是一個綜合題(?)，有點呼應到前面的 DFS 和 Backtracking(?)。

所以首先我們需要建立 Trie，這裡使用一般的 Object 來建立(假設 isEnd 代表是不是結尾，也就是有沒有值在這個節點上)

const trie = {}
for (const path of folder) {
    let ptr = trie // 指標，類似 linked-list 的操作手法
    const names = path.slice(1).split('/') // 題目保證第一個字元是 `/`，所以可以直接略過再來切割
    for (let i = 0; i < names.length; i++) { // 逐層建立
        const name = names[i] // 取得名稱
        ptr[name] = ptr[name] || { children: {}, isEnd: false } // 如果不存在就建立
        if (i === names.length - 1) ptr[name].isEnd = true // 如果是最後一層就設定為有值
        ptr = ptr[name].children // 指標移到下一層
    }
}

這樣子如果你印出 trie 的話，應該會長得像這樣:

{
  "a": {
    "children": {
      "b": {
        "children": {},
        "isEnd": true
      }
    },
    "isEnd": true
  },
  "c": {
    "children": {
      "d": {
        "children": {
          "e": {
            "children": {},
            "isEnd": true
          }
        },
        "isEnd": true
      },
      "f": {
        "children": {},
        "isEnd": true
      }
    },
    "isEnd": false
  }
}

上面這個資料結構應該滿好理解的，接著就是以 DFS 的方式走訪，只要碰到 isEnd 是 true 的節點，就可以把他的路徑加到結果中並跳出遞迴。

const output = [] // 結果
const dfs = (node, path) => { // DFS
    if (node.isEnd) { // 如果是結尾(有值)
        output.push(path) // 加到結果中
        return // 跳出遞迴
    }

    for (const name in node.children) { // 逐個走訪
        dfs(node.children[name], path + '/' + name) // 往下走
    }
}

for (const name in trie) { // 逐個走訪
    dfs(trie[name], '/' + name) // 從第一層開始
}

這時 output 就是答案了。

然而這題呢，如果是練手的話，可以自己像上面一樣實作 Trie 的資料結構，但常常 Trie 的題目不見得需要建立 Trie，有時候只是需要用到 Trie 的特性，舉例來說，這題其實可以不用建立 Trie，只要排序完找前綴就可以了。

舉例來說:

folder = ["/a","/a/b","/c/d","/c/d/e","/c/f"]

其實就是 /a 一定會採用，然後之後開始照下面步驟檢查:

• /a/b 發現和 /a 相同前綴，所以不處理
• /c/d 發現和 /a 不同前綴，所以加入答案
• /c/d/e 發現和 /c/d 相同前綴，所以不處理
• /c/f 發現和 /c/d 不同前綴，所以加入答案

這樣就可以得到答案了，寫起程式起來也簡單很多:

const sortedFolder = folder.sort() // 先排序
const result = [sortedFolder[0]] // 第一個一定要加入，因為排序過，他一定是最上層的資料夾

for (let i = 1; i < sortedFolder.length; i++) { // 接著從第二個資料夾開始檢查
    // 如果當前的資料夾不屬於最後一個答案的前綴，就加入答案
    if (!sortedFolder[i].startsWith(result[result.length - 1] + '/')) {
        result.push(sortedFolder[i])
    }
}

return result

這邊的後綴 / 很重要，否則可能會有誤判，所以要注意。

例如: /a 和 /ab，如果你沒有在後綴加上 /，那他們會被誤判成前綴相同，這樣就不對了。

二元樹(Binary Tree)

最最最後，以最常見的 Binary Tree 來做結尾，不多說直接上題目。

題目: 2458. Height of Binary Tree After Subtree Removal Queries

這題是這樣子的，給你一個二元樹，問你我刪除特定節點之後，樹的高度是多少。

嗯...聽起來很簡單，但卻是一個很有挑戰性的題目，需要運用到你的資料結構的底子(?)

我不敢說寫得多漂亮，但我可以稍微用描述的XD (<-- 也許 Editoral 會有更好的解法，更漂亮的寫法，但我還沒去拜讀他)

所以這邊提供我「直覺」的解法供參考(?)

題目要包含子樹一起刪除，然後看刪除後的樹高，所以直覺就是從你刪除節點後重新找樹高。不過這樣的話每次都要重新找一次樹高，花費一次 O(n) 的時間，這樣的話就會變成 O(n^2) 的時間複雜度，這樣是不行的。

雖然題目的查詢次數 m，最大是到 10^4，但是 n 最大是 10^5，所以無論如何 10^9 是絕對會超時的。

所以就必須減少查詢樹高的時間，這時就可以從刪除的節點開始往上找，不過單純的往上找也不行，因為最壞情況刪除的節點是最下面的然後又是歪斜樹的話，單次查詢又回到了 O(n) 的時間複雜度。

這時可以找到需要重新計算的節點(我先暫時用 ancestor 稱呼)，然後從這個節點往上跳，這樣就可以減少查詢的時間。

那麼怎麼確定哪些節點是需要重新計算的呢? 答案是有分岔的節點就需要重新計算，為什麼?

可以想像一下，當你刪除的節點有兄弟的時候，刪除你可能根本不影響樹高，因為你兄弟可能比你還高，反之如果你是孤兒(?)，只有你一個兒子的時候，刪掉你就會影響樹高(至少對於你的 ancestor 來說)，但說不定到更上層的 ancestor 來說他根本不在乎，所以這些 ancestor 才需要重新計算。

我知道可能講成這樣可能有點抽象，所以畫些圖來看看:

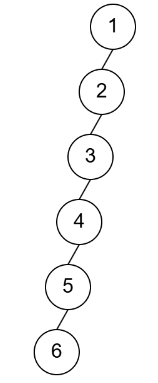
假設今天樹是歪的，你刪除的節點在歪斜的樹當中的其中一個，你根本沒必要檢查父節點，直接一路跳到最上面就好，因為他重新計算後就可以了，重新計算中間的節點都是額外的浪費。

看懂了第一種情況之後，來看一張比較大的圖

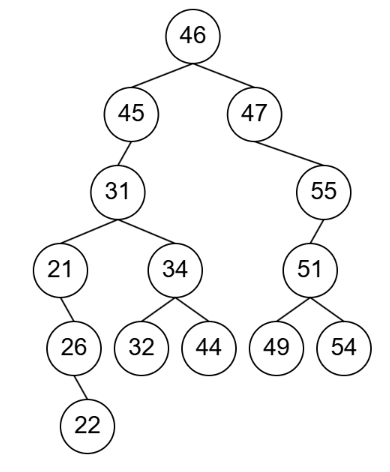
假設我刪在一樣是歪斜的節點上，假設我刪除左下角的 22，根據上面說明的情況，一路跳到 31 重新計算就好，因為中間的 26、21 都不重要。

那麼如果我刪除右下的 54 呢?，因為他有兄弟，所以只會跳到上一層 51，接著 51 並沒有兄弟，就一路往上跳到有兄弟節點的父節點 46 來計算即可。

這麼做的話就可以將重新計算的時間複雜度降低至 O(logn)。

這個 O(logn) 是怎麼來的呢? 很簡單，讓我們攤開來看:

• 假設樹是歪斜的: 一瞬間跳到頂，你姑且可以說他 O(1)
• 假設樹是平衡的: 一路往上跳，最多跳 logn 次，所以是 O(logn)
• 假設樹亂長: 界於 O(1) 和 O(logn) 之間 ~= O(logn)

所以這樣的話就可以將整體時間複雜度降低至 O(nlogn)，這樣就可以接受了。

如果有學過一點資料結構或演算法的人，可能會覺得這個似曾相似(?)，有點像找關節點(articulation point)的做法，然後這些關節點(這邊先稱呼為 ancestor)就是需要重新計算的節點。

所以我的想法是，先走一次 dfs 把該計算該連起來該存的都處理好，之後查詢時動態的去計算樹高，這樣就可以達到目的了。

我姑且將這個 dfs 取名叫做 connected(?)，這個 connected 函數會將我的樹當中的每個節點增加一些屬性:

• l: 左子樹高
• r: 右子樹高
• depth: 深度
• ancestor: 需要重新計算的祖先節點(關節點)
• dir: 方向(通往祖先的方向)

然後還有一個 map 去存放每個節點的參考，這樣在之後查詢可以直接取得節點，增加速度。

const map = {}
const connected = (node, ancestor = node, dir = '', depth = 0) => {
    if (!node) return 0
    map[node.val] = node // 存放節點
    node.ancestor = ancestor // 設定祖先
    node.dir = dir // 設定方向
    node.depth = depth // 設定深度
    if (node.left && node.right) { // 如果左右都有小孩
        node.l = connected(node.left, node, 'r', depth + 1) + 1 // 計算左子樹高
        node.r = connected(node.right, node, 'l', depth + 1) + 1 // 計算右子樹高
        return Math.max(node.l, node.r) // 回傳樹高(最大值)
    } else if (node.left) {
        node.l = connected(node.left, ancestor, dir || 'r', depth + 1) + 1 // 計算左子樹高
        node.r = 0 // 右子樹高為 0
        return node.l // 回傳左子樹高(最大值)
    } else if (node.right) {
        node.l = 0 // 左子樹高為 0
        node.r = connected(node.right, ancestor, dir || 'l', depth + 1) + 1 // 計算右子樹高
        return node.r // 回傳右子樹高(最大值)
    } else {
        node.l = 0 // 左子樹高為 0
        node.r = 0 // 右子樹高為 0
        return 0 // 回傳 0(樹高)
    }
}
connected(root)

這樣的話，每個節點都會有這些屬性，之後查詢的時候就可以直接取得，然後動態的計算樹高，就不用每次都在往回走重新計算了。

接著就可以開始做查詢的部分:

const output = [] // 結果
const memo = {} // 空間換取時間，記錄查詢過的結果
for (const query of queries) {
    // 如果查詢過就直接取出
    if (typeof memo[query] !== 'undefined') {
        output.push(memo[query])
        continue 
    }

    const node = map[query] // 取得節點
    let height = 0 // 預設樹高為 0
    let dir = node.dir // 當前要往祖先的方向
    let depth = node.depth // 當前節點所在的深度
    let ptr = node.ancestor // 指標從祖先開始
    let prev = depth - ptr.depth - 1 // 計算祖先和當前節點的深度差以取得樹高
    let flag = true // 至少跑一次
    while (flag) {
        if (ptr === root) flag = false // 如果到根節點，下一次就停止
        // height 為當前樹高
        // prev 為刪減節點後的方向的子樹高
        // ptr[dir] 為祖先的 prev 另一邊的子樹高
        height = Math.max(height, prev, ptr[dir])
        depth = ptr.depth  // 更新深度
        dir = ptr.dir // 更新方向
        ptr = ptr.ancestor // 更新指標(往上跳)
        prev = height + depth - ptr.depth // 計算新的 prev
    }

    height = Math.max(height, prev) // 更新最大樹高

    memo[query] = height // 先紀錄起來
    output.push(height) // 加到結果中
}

也許在 while 迴圈當中的計算有點複雜，但可以用下面這一張圖來幫助理解:

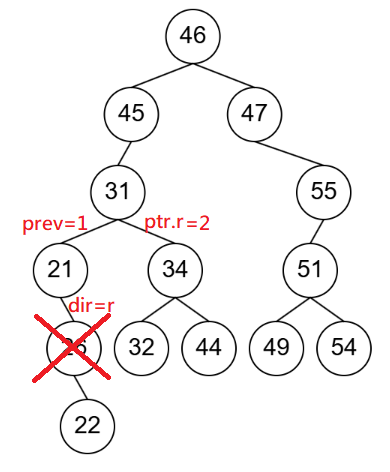
假設我刪除的是 26，那麼當時那邊的 dir 就是 r，代表我要從祖先的右子樹拿樹高和 prev(刪除節點方向刪除後的子樹高)來比較，留下比較高的那個，然後一路往上計算。

神奇的 Daily

一開始在前言所提到的神奇的問題到底是什麼呢?

其實說不定這並不神奇，只是我第一次碰到

先講結論，2024/08/27 原本的 daily 消失了，不知道有沒有跟我一樣有在那一天解 daily 的人有發現那一天的 daily 被掉包了(?)

原本的題目是: 1514. Path with Maximum Probability

被替換成: 1. Two Sum

不相信的話你去找看看 2024/08/27 的 daily 是不是 Two Sum，然後你看看我下面這張截圖:

我在 2024 根本沒碰那題，然後看看我的八月份的 daily:

然後看看我的 Submissions: (2024/08/26 至 2024/08/28)

可以自己去看看 2024/08/26 和 2024/08/28 的 daily 是不是正確的，然後你看看我中間唯一送的 Submission 就是 Path with Maximum Probability，足以證明 2024/08/27 的 daily 被換掉了XD。

至於我是怎麼發現這件事的呢?

其實是我在隔天搭車的時候在想有沒有更好的解法，然後後來想回來嘗試，結果，「蛤」，怎麼是 Two Sum...，我不記得我有解這題阿

事情經過就是這個樣子~

結語

這篇大概節錄了一些這一年來 LeetCode Daily 的精選(?)題目，希望明年差不多時間還有一樣的文章(代表又堅持了一年(?))

不過老實說，如果真的希望有明顯進步的話，一天一題肯定是不夠的，至少我這一年來的感受是這樣，和以前當選手時相比，一天解很多題的感受真的是差很多。

不過這樣的進步也是有的，只是這個幅度可能就比較小，但是這樣的進步也是進步，畢竟每天進步一點點，累積起來也是很可觀(?)。

以為我會說明年的目標是再維持一年的 LeetCode Daily 嗎? 不不不，這是基本的，我比較希望我明年能夠順利早點畢業。